MOTION FORCES & ENERGY
Physical quantities and measurement techniques
Length
To measure length we use meter rule , measuring tape. For length that are very small we use micrometer screw gauge.
Range and precision
-
Meter rule - Up to a meter, can be used to measure length between 1mm to 1m (E.g The length of a book)
-
Measuring tape - Up to several meters, can be used to measure length between 1mm to several meters (E.g The length of a side of room)
-
Micrometer - Less than a centimeter , can be used to measure length between 0.01mm to several meters (E.g The diameter of wire)

Measuring the volume of an irregularly shaped object.
-
For an object that is irregularly shaped, it is placed in a measuring cylinder containing water.
-
To find out the volume of the object the difference between the final and initial volume is found.
-
In the diagram above the initial reading is 50 cm and the final reading is 60 cm .
-
By subtracting the final value (60cm )from the initial (50cm )one we get the volume of the object (10cm ).
3
3
3
3
3
During this sort of experiment parallax error is one of the main source for anomalies. For paper 4 make sure you mention it.
Time
-
Interval of time is measured using clocks or a stopwatch
-
SI unit for time is the second(s)
-
To find the amount of time it takes a pendulum to make a spin, time ~25 circles and then divide by the same number as the number of circles.
Micrometer
The labelled diagram of a micrometer is shown below.

Step 1
Find the main scale reading.
-
It is the closest line to the thimble scale.
-
Every small box in a micrometer main scale represents 1mm.
-
In the above image the main scale reading is 7.5 mm.
Step 2
-
Find the thimble scale reading.
-
This is the line that intersects with the datum line(the horizontal line on main scale).
-
In the figure above it is 24.
-
Every unit in the thimble scale is 0.01mm
-
So we need to multiply the reading with 0.01mm.
Step 3
-
Multiply the thimble scale reading with 0.01 , 24 x 0.01 = 0.024mm.
Step 4
-
Add the two values here, 7.5 + (0.001)x 24 = 7.524mm
-
Sometimes a micrometer may be faulty!
-
It may show a zero error.(Reading shown when there is nothing given to measure).
-
For this situation we need to add or subtract the initial reading (zero error).
Another example

Reading of main scale = 7.5 mm
Reading of thimble scale = 14mm
Multiply the thimble scale reading with 0.01 so 14 x 0.01 = 0.14mm
Add the two readings together
7.5 mm + 0.14 mm = 7.64mm
Scalar Quantity: Quantities that have a magnitude only. Example : distance, speed, time, mass, energy and temperature.
Vector Quantity: Quantities that have both a magnitude and a direction . Example :displacement, force, weight, velocity, acceleration, momentum, electric field strength and gravitational field strength
Vectors

-
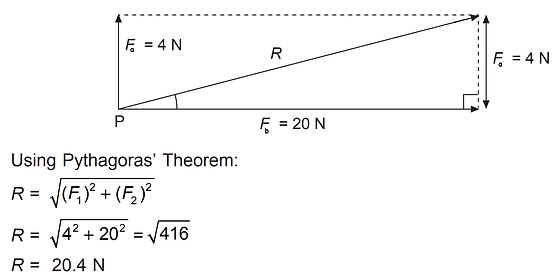
Select an appropriate scale E.g. 1 cm to 2 N.
-
Step 2: Draw a parallelogram of vectors to scale.
-
Step 3: Measure the diagonal to find R(AB)
Pythagorean theorem can be used if is a right angled triangle.
Steps to find the period of oscillation:
Step 1: Take the total time for multiple oscillations (E.g 20).
Step 2: Repeat Step 1.
Step 3: Take the average of the two timings.
Step 4: Divide the average in Step 3 by the number of oscillations ( here 20) to obtain the period.
Motion
Distance vs Displacement : Distance is the length between two points , displacement is the length between two points in a specific direction.
Speed : The rate of change of distance per unit time.
Velocity: The rate of change of displacement per unit time.
Speed =
Distance
Time
Velocity =
Displacement
time
Average Speed =
Total distance
Total time
Acceleration : The of change of velocity per unit time.
Acceleration=
Change in Velocity
Time taken
Uniform acceleration: Uniform acceleration is a type of motion where the acceleration is constant. E.g An object falling from rest on earth in vacuum.
Non - uniform acceleration: Non - uniform acceleration is a type of motion where the acceleration is not constant. E.g A parachutist falling freely in air, here the acceleration starts with 9.8m/s and eventually turns to zero.
2
Deceleration : It is a negative acceleration.

-
The gradient of a distance time graph represents the speed of the body.

-
The gradient of a velocity time graph represents the acceleration of the body.
-
The area under the velocity time graph represents the displacement of the body.

The distance time graph for the motion of a car is given below.

-
To find the speed of the car the gradient of the graph is calculated.
Step 1
Find the change vertically.
Step 2
Find the change horizontally.
Step 3
Use the formula Gradient = Vertical change / Horizontal change
Here ,
The vertical change (height) is 60 m.
The horizontal change (width) is 5s.
So, gradient is 60/5 = 12
As the gradient is the speed of the car so the speed will be 12 m/s.
Sometimes in exam the units might be different. Make sure to convert the units
-
Convert meters(distance) and seconds (time)for m/s.
-
Convert km(distance) and hours(time) for km/h.
The velocity time graph for the motion of a car is given below.

-
To find the displacement of the car area under the graph is calculated.
-
For the time from 0 to 5 seconds the displacement is the area under the triangle.
-
We use the formula to find the area under the triangle, x 5 x 10 = 25
1
2
-
For the time from 5 to 10 seconds the displacement is the area under the rectangle.
-
We use the formula to find the area under the rectangle, (10-5) x 10 = 50
-
Our total displacement from t= 0 to t = 10 is 25 + 50 = 75m
Mass and weight
-
Mass is a measure of the quantity of matter in an object at rest relative to the observer.
-
Mass of an object resists change from its state of rest or motion. This is known as inertia.
-
Weights, and therefore masses, may be compared using a beam balance or equal-arm balance.
Using an electronic balance
-
Zero the scale or press the tare button. The balance should read "0".
-
Measure the mass of the sample.
-
Repeat the process and take several readings.
-
Take the average reading.
Using a force meter
-
Hold the forcemeter vertically.
-
Pull on the spring with a force of 1 newton.
-
Hang another mass from the forcemeter.
-
Repeat this up to 10 newtons.
-
Take the masses off the forcemeter and hang the unknown mass from it.
Gravitational field strength : Gravitational field strength is the force per unit mass.
-
Gravitational field strength is equivalent to the acceleration of free fall.
-
A gravitational field is a region in which a mass experiences a force due to gravitational attraction
Gravitational field strength (g) =
Weight (W)
Mass (m)
Density
Density: Density is mass per unit volume.
Density(ρ) =
Mass(m)
Volume(V)
Determining the density.
Liquid
-
Take an empty measuring cylinder.
-
Put it on an electronic balance and record its mass.
-
Pour the liquid in the cylinder and record the mass of both liquid and cylinder.
-
Record the volume on the measuring cylinder.(Repeat this process and take the average value to minimize the effect of parallax error).
-
Subtract the mass of cylinder from the total mass (liquid + cylinder) to get the mass of only liquid.
-
Use the formula for density to find the average density of the liquid.
Regularly shaped solid
-
Take the solid and measure its dimensions. (For sphere measure the diameter or for a cube measure the sides and height).
-
Use the dimensions to calculate the volume of the solid.
-
Place the solid on an electronic balance and record the reading.
-
Divide the value of mass by volume to get density.
An irregularly shaped solid
-
Take the solid and put it on an electronic balance and record the reading.
-
Take a measuring cylinder and pour water in it.
-
Put the solid in the measuring cylinder that contains water.
-
Record the increase in volume.(This is the volume of the solid)
-
Divide the value of mass by volume to get density.
Make sure you measure the mass
before placing it into water.
Measuring mass after placing into water will add extra mass of water.
Forces
Force:Force is the push or pull on an object with mass that causes it to change its velocity (accelerate).
Some examples of force are weight (gravitational force), friction, drag, air resistance, tension (elastic force), electrostatic force, magnetic force, thrust (driving force) and contact force.
Newton’s first law :An object either remains at rest or continues to move in a straight line at constant speed unless acted on by a resultant force.
Newton’s third law: When object A exerts a force on object B, then object B exerts an equal and opposite force on object A.
-
A force may change the velocity of an object by changing its direction of motion or its speed.
-
Newton’s third law describes pairs of forces of the same type acting on different objects.
Finding the resultant force

Resultant force = mass × acceleration
F = ma
Friction
Friction : A force that may impede motion and produce heating.
Terminal Velocity
-
When an object falls freely in a fluid (liquids or gases) it reaches terminal velocity.
-
The acceleration of every object starts with 9.8 m/s initially.
-
As time proceeds the force due to resistance increases (air resistance in air and drag in liquid).
-
Resistance increases with velocity.
-
Increase of resistance decreases the resultant force.
-
As resultant force decreases the acceleration also decreases.
-
Eventually the acceleration reaches zero and the object reaches terminal velocity.
-
Reaction time is the time for a driver to react to a situation and apply the brakes.
-
The thinking distance is the distance travelled in his/her reaction time.
-
Stopping distance is the distance covered between the time when the body decides to stop a moving vehicle and the time when the vehicle stops entirely.
-
Factors which affect thinking distance are tiredness, speed or under the influence of drugs or alcohol.
-
Factors which affect breaking distance are mass of the car, tyre surface and road conditions.
Elastic deformation
Forces can only produce a change in size and shape of an object but no change in mass or weight.
Spring constant :Spring constant is the force per unit extension.
Spring constant(k) =
Force(F)
Extension(K)
Graph of Hooks law

-
As k is constant , the ratio of force to extension of a spring will be the same between the region that obeys Hookes law.

Remember!
-
The gradient of a force extension graph is the spring constant k.
-
The steeper a graph is the higher the value of k.
-
The value of spring constant k defines how stiff the elastic is.
Determining the spring constant (k ) of a spring.
-
The spring is taken and hung vertically.
-
Different weights are hung form the spring.
-
The weights are recorded.
-
The extension of the spring is calculated by finding the difference between initial and final length.
-
A graph of force (against y-axis) and extension (x-axis) is plotted.
-
The gradient of the graph is found which is the spring constant k.
Limit of proportionality: Limit of proportionality is the point up to which extension is directly proportional to force (obeys Hooks law).
Circular motion
Motion in a circular path due to a force perpendicular to the motion has the following properties.
-
speed increases if force increases, with mass and radius constant.
-
radius decreases if force increases, with mass and speed constant.
-
an increased mass requires an increased force to keep speed and radius constant.
Turning effect of forces
-
The moment of a force is a measure of its turning effect.
-
The moment of a force is = force × perpendicular distance from the pivot.
-
The principle of moment states that for an object in equilibrium the total clockwise moment will be equal to the total anticlockwise moment.

F × a = F × b
1
2
Experiment to verify the principle of moment.
-
A meter rule is placed on a pivot.
-
Objects of known masses are attached to opposite ends of the rule.
-
The masses are adjusted until the rule is balanced.
-
Increasing the weight the process is repeated several times.
-
The masses and their distance(a and b) of them from the pivots are recorded.
-
The moment is calculated by the formula M = W × d.
-
It will be observed that every time the rule balances the total clockwise moment equals the total anticlockwise moment.
Centre of gravity
Centre of gravity: Centre of gravity is a point from which the weight of a body or system may be considered to act.

Determine the position of the centre of gravity of a plane lamina
-
Make three holes near the edge of the lamina. (They should be as far as possible from one another).
-
Suspend the lamina freely from a pin.
-
Hang a plumb line from the pin in front of the lamina.
-
After the plumb line becomes steady, trace the line on the lamina.
-
Repeat the steps above for the other two holes.
-
The point on which the three lines intersect is the centre of gravity.
The stability of an object is affected by
-
position of the centre of gravity
-
the surface area of contact.

Momentum
-
Momentum : Momentum is mass × velocity. p = mv, where p is momentum.
-
Impulse : Impulse is force × time, for which force acts.
-
Impulse = F x t = Δ(mv) or change in momentum.
-
Resultant force: Resultant force is the change in momentum per unit time.
Resultant force(F ) =
Change in momentum(Δp)
Time (∆t)
The principal of conservation of momentum The principal of conservation of momentum states that when two particles collide in a closed system, the total momentum before collision and after collision is the same.


-
The total momentum of the system before the gas molecule collides with the wall remains same after collision.
-
Momentum of gas molecule p= m x v where m is the mass of gas molecule and v is the velocity.
-
Momentum of the wall is “Zero” as it is stationary.
Example 1
A ball of mass 6kg moves towards another ball of mass 4kg with initial velocity of 6m/s. The second ball was stationary before collision. After collision they stick together and move off with a common velocity. Calculate the common velocity.
Solution

Example 2
A particle of mass 2kg collides with a wall with a velocity of 10m/s. It rebounds within 0.2s after colliding. Calculate the force it exerts on the wall.

Energy, work and power
Energy
-
Energy may be stored as kinetic, gravitational potential, chemical, elastic (strain), nuclear, electrostatic and internal (thermal).
Energy is transferred between stores during events and processes.
Examples
-
In a hydroelectric power station, the gravitational potential is converted to kinetic energy and then finally to electrical energy.
-
When a parachutist falls freely under gravity at terminal velocity gravitational potential energy is converted to thermal energy.(kinetic energy stays constant as there is no change in velocity).
-
In solar panels light energy is converted to electrical energy.
The principle of energy conservation: The principle of energy conservation states that energy is neither created nor destroyed. It may transform from one type to another

Work
Work done = force × distance moved in the direction of the force
W = F × d
Energy resources
-
Renewable resources include hydroelectric, wind, and solar , tidal.
-
Nonrenewable resources include coal, natural gas and nuclear.
Generating electricity.
-
Chemical energy stored in fossil fuels Heat Kinetic energy of steam Kinetic energy of turbine Electrical energy.
-
Potential energy of water Kinetic energy of water Kinetic energy of turbine Electrical energy
-
In solar light energy from sun is converted to electrical energy.
Renewable energy resources are better than non-renewable resources as
-
they can be used repeatedly
-
they have a less harmful effect on the environment
-
they are always available
(%) efficiency =
(useful energy output)
(total energy input)
( × 100%)
(%) efficiency =
(useful power output)
(total power input)
( × 100%)
Power
Power: Power is work done per unit time or energy transferred per unit time.
Power(P ) =
Work done(W)
Time (t )
Power(P ) =
Energy transferred(∆E)
Time taken (t )
Pressure
Pressure: Pressure is force per unit area.
Pressure(P ) =
Force(F )
Area(A )
The lower the area the higher the pressure.
The higher the force the higher the pressure.
Example:
An elephant weighing 4000kg and the total surface area in contact with the ground is 0.3m , a woman weighing 50kg wearing a heel with a surface area of 4 x 10 m .
By calculation find out who exerts more pressure.
2
2
-10
Use the formula for pressure
Pressure(P ) =
Force(F)
Area(A)
For elephant , pressure = 4000 x 9.8 / 0.3 (Note that we take the weight not mass)
= 130 KN/m
2
For woman, pressure = 50 x 9.8 / 4 x 10
= 1.2 x 10 KN/m
9
-10
2
-
Pressure at a surface produces a force in a direction at right angle to the surface.
-
The height of a liquid column may be used to measure the atmospheric pressure (e.g mercury barometer).
-
Atmospheric pressure acts on the surface of the mercury.
-
The height h indicates the atmospheric pressure.
-
If the atmospheric pressure increases the height h will decrease.

-
The pressure in a liquid increase with depth.
-
At greater depths, the weight of the liquid above it is greater, so the pressure is greater.
-
The density of liquid also contributes to the pressure.
-
High density of the liguids results in more pressure.

change in pressure = density × gravitational field strength×change in height
∆p = ρg∆h