Distance:
The total length of the path taken by an object is called distance. It is a scalar quantity and has only magnitude.
Example: If a car moves 50 km from point A to point B and then comes back to point A, then the distance traveled is 100 km.
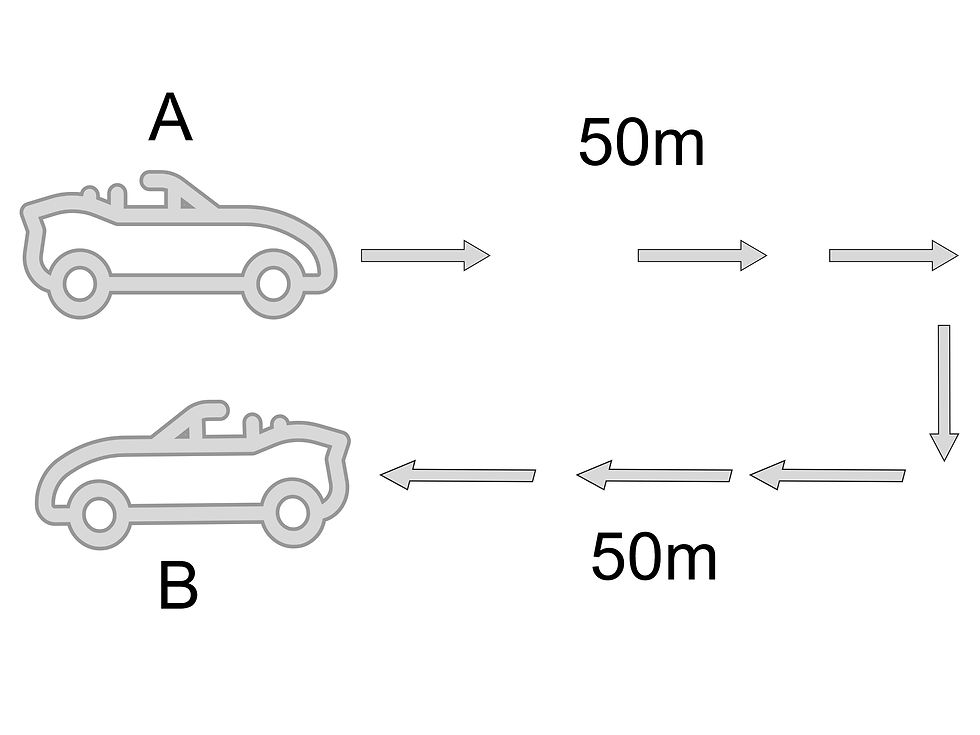
Displacement:
The change in position of an object from its initial position to the final position is called displacement. It is a vector quantity and has both magnitude and direction.
Example: If a person walks 10 meters north and then 10 meters south, then the displacement is zero because the final position is the same as the initial position.
Speed:
The rate at which distance is covered by an object is called speed. It is a scalar quantity and has only magnitude.
Example: If a car covers 100 km in 2 hours, then the speed is 50 km/h.
Velocity:
The rate at which displacement is covered by an object is called velocity. It is a vector quantity and has both magnitude and direction.
Example: If a person walks 10 meters north in 2 seconds, then the velocity is 5 m/s towards north.
Acceleration:
The rate at which velocity changes with time is called acceleration. It is a vector quantity and has both magnitude and direction.
Example: If a car increases its velocity from 0 to 50 km/h in 10 seconds, then the acceleration is 5 km/h/s.
Graphical method
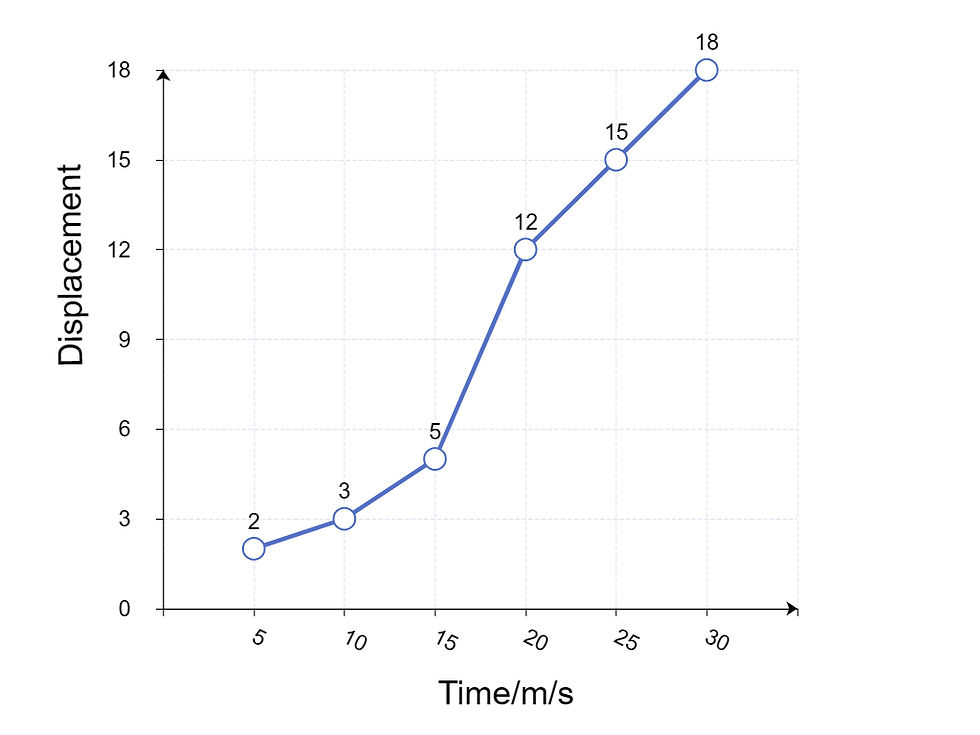
The gradient of a displacement time graph gives us the velocity of the body.
To find the gradient of the line passing through the points (20,12) and (30,18), we use the formula:
m = (y₂ - y₁) / (x₂ - x₁)
where m is the gradient, (x₁, y₁) and (x₂, y₂) are the coordinates of the two points.
Substituting the values, we have:
m = (18 - 12) / (30 - 20) m
= 6 / 10 m
= 0.6
Therefore, the gradient of the line passing through the points (20,12) and (30,18) is 0.6. And the velocity of the body is 0.6 m/s.
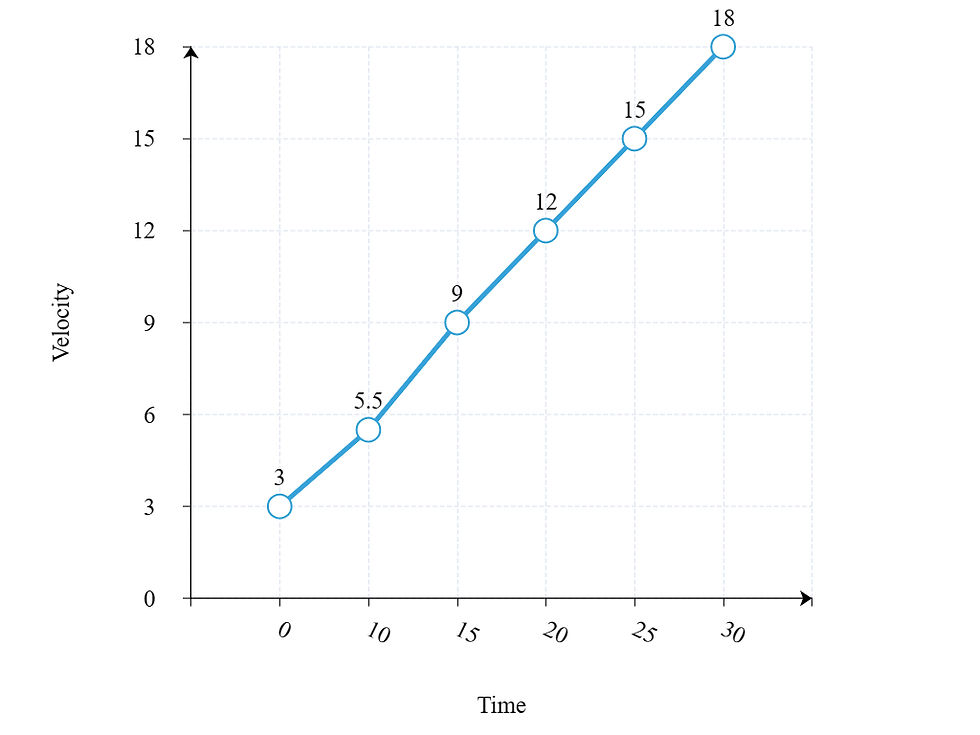
Area under the velocity-time graph gives us the distance of the body.
To find the distance travelled by the body from time 15 to 30, we need to use the parallelogram formula.
A = 1/2 x (a + b) x h
Comments