Quadratic functions are of the form y = ax² + bx + c .
A quadratic function has a maximum or a minimum value, and its graph is symmetrical.
EXAMPLE
(a)6x² + 5 = 17x
(b) 9x² -39x -30 = 0
(c) A rectangle has sides of length x cm and (6x − 7) cm. The area of the rectangle is
90 cm² Find the lengths of the sides of the rectangle.
The quadratic formula
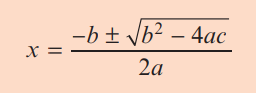
EXAMPLE
(a) Solve 6x² + 5x+3 = 0 for x.
Hint:Here a = 6 ,b= 5, c = 3
Solving simultaneous equations using the graphical method
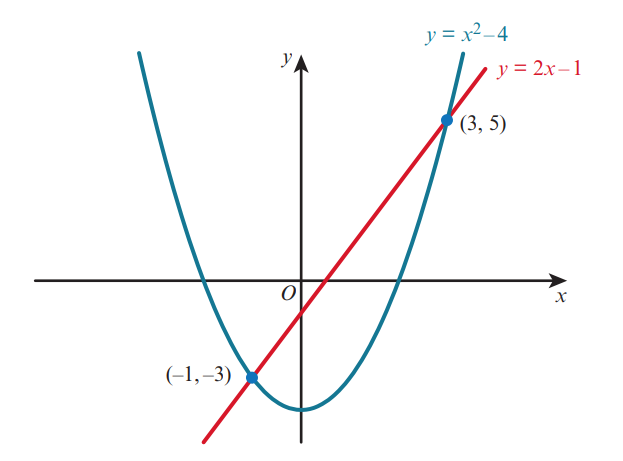
The diagram shows the graphs of y =x² -4 and y=2x-1.
The coordinates of the points of intersection of the two graphs are ( 1− −, 3) and (3, 5).
x=-1 , y= -3 and x = 3,y=5 are the solutions of the simultaneous.
Algebraic solution
y =x² -4 and y=2x-1.
Substitute a variable,
x² -4 = 2x-1
Rearranging and factorising gives x=-1 , y= -3 and x = 3,y=5 as solutions
Complex forms:
Example :
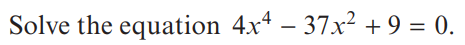
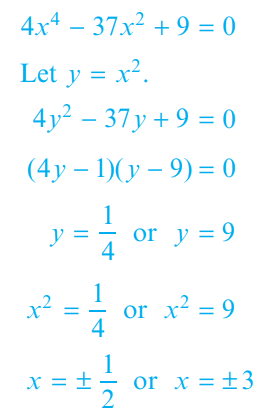
Comments