Physical quantities

All physical quantities consist of a numerical magnitude and a unit.
Some SI base quantities and their units:
Mass (kg)
Length m)
Time (s)
Current (A)
Temperature (K).

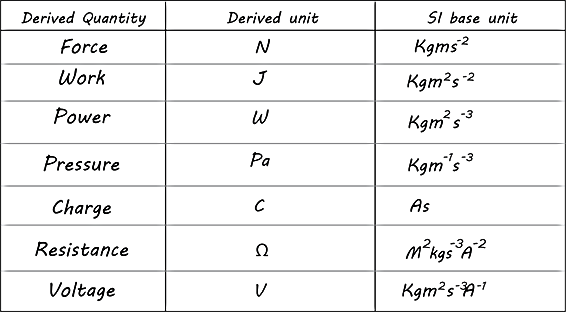
Some derived units

Homogeneity

An equation is considered homogeneous if both sides of the equation have the same units.

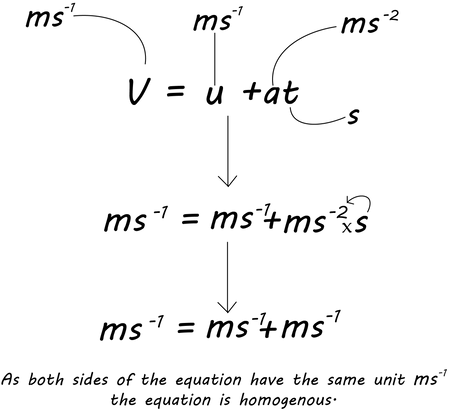
Prefixes

Systematic errors: Errors in a measurement that is caused by a faulty system.
Systematic errors always vary by a constant amount.
Systematic errors can not be avoided by taking an average value.
Examples include zero error.

Random errors: Errors in a measurement that is caused by any factor that can vary from one experiment to other.
Random errors do not differ by any constant amount but are scattered around the actual reading.
Random errors can be avoided by taking an average value.
Examples include parallax error

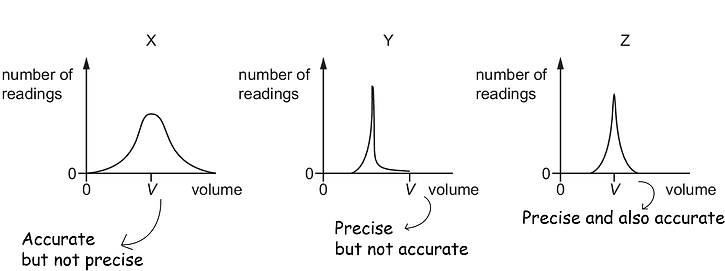
Precision: Measurements with the least range.

Accuracy: It is the reading that is closest to the actual value.

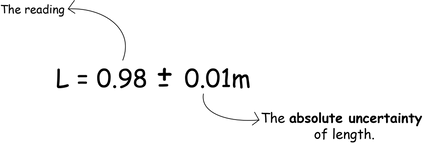
Uncertainty

Fractional uncertainty=

Absolute uncertainty

Measured value

Percentage uncertainty (%)=

Absolute uncertainty

Measured value

x 100

Uncertainty is always added.
Uncertainty of power function is found by multiplying the uncertainty of quantity by power.
There is no uncertainty for constant factors.

Remember!

Absolute uncertainty is always expressed in one significant figure.

Example: 1

The velocity of a car is 5.6 ± 2 m/s. The time taken for it to move a distance was 0.8 ± 0.01 s.

Calculate the fractional uncertainty in the value of acceleration.

To find the fractional uncertainty in the value of acceleration we need to add the fractional uncertainties of velocity and time.

To find the fractional uncertainty in the value of acceleration we need to add the fractional uncertainties of velocity and time.
To find the percentage uncertainty in the value of acceleration we need to add the percentage uncertainties of velocity and time.

fractional uncertainty of velocity = 2/5.6 = 0.357
fractional uncertainty of time = 0.01/0.8 = 0.0125

So,

fractional uncertainty of acceleration = 0.357 + 0.0125 = 0.37

To find the percentage uncertainty multiply the fractional uncertainty by 100.

Example: 2

The base of a cylinder has a radius of 3 ± 0.2 cm and a height of 10± 1 cm .

Calculate the volume of the cylinder with its absolute uncertainty.

Volume = π r × h

The value of the highest power contributes the most to the uncertainty in any given equation.

Here,

fractional uncertainty of volume = 2 × fractional uncertainty of radius + fractional uncertainty of height.

fractional uncertainty of radius = 0.2 / 3

fractional uncertainty of height = 1 / 10

fractional uncertainty of volume = (0.067 × 2)+ 0.1 = 0.234

Volume = 282.74

Absolute uncertainty of volume = fractional uncertainty × the value of the volume.

= 0.234 × 282.74

= 66.16

Finally ,

Volume = 280 ± 70 cm

Scalar Quantity: Quantities that have a magnitude only. Example : distance, speed, time, mass, energy and temperature.

Vector Quantity: Quantities that have both a magnitude and a direction . Example :displacement, force, weight, velocity, acceleration, momentum, electric field strength and gravitational field strength

Vectors

Select an appropriate scale E.g. 1 cm to 2 N.
Step 2: Draw a parallelogram of vectors to scale.
Step 3: Measure the diagonal to find R(AB)

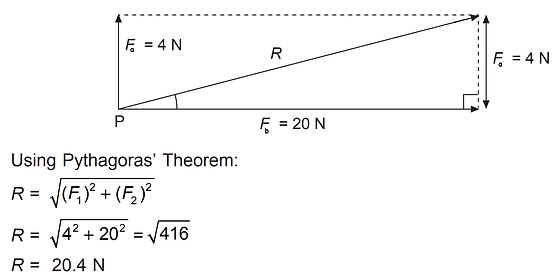
Pythagorean theorem can be used if is a right angled triangle.

Steps to find the period of oscillation:

Step 1: Take the total time for multiple oscillations (E.g 20).

Step 2: Repeat Step 1.

Step 3: Take the average of the two timings.

Step 4: Divide the average in Step 3 by the number of oscillations ( here 20) to obtain the period.

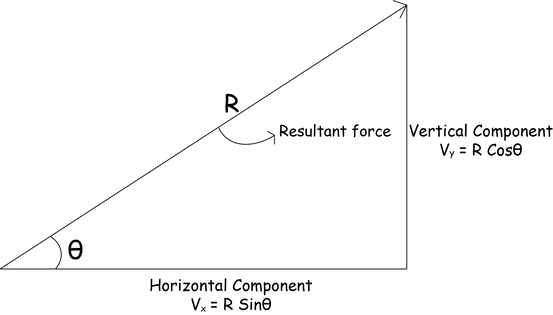
Resolving forces

A force can be resolved into two perpendicular components.

For the horizontal component, it is R Sinθ.

For the vertical component, it is R Cosθ.

Get PDF